力扣第240场周赛

题一 人口最多的年份

描述

给你一个二维整数数组 logs ，其中每个 logs[i] = [birthi, deathi] 表示第 i 个人的出生和死亡年份。

年份 x 的 人口 定义为这一年期间活着的人的数目。第 i 个人被计入年份 x 的人口需要满足：x 在闭区间 [birthi, deathi - 1] 内。注意，人不应当计入他们死亡当年的人口中。

返回 人口最多 且 最早 的年份。

示例 1：

输入：logs = [[1993,1999],[2000,2010]] 输出：1993 解释：人口最多为 1 ，而 1993 是人口为 1 的最早年份。 示例 2：

输入：logs = [[1950,1961],[1960,1971],[1970,1981]] 输出：1960 解释： 人口最多为 2 ，分别出现在 1960 和 1970 。 其中最早年份是 1960 。

提示：

1 <= logs.length <= 100 1950 <= birthi < deathi <= 2050

思路

用一个数组存储所有年份出生的人数减去去世的人数，然后遍历得到人口最多的年份。

代码

package JavaCode.contest.weekly.n201_300.n240;

public class N1 {
    public int maximumPopulation(int[][] logs) {
        int[] book=new int[101];
        for (int[] log:logs){
            book[log[0]-1950]++;
            book[log[1]-1950]--;
        }
        int s=0;
        int max=0;
        int res=1950;
        for (int i=0;i< book.length;i++){
            s+=book[i];
            if(max<s){
                max=s;
                res=i+1950;
            }
        }
        return res;
    }
}

题二 下标对中的最大距离

描述

给你两个 非递增 的整数数组 nums1 和 nums2 ，数组下标均 从 0 开始 计数。

下标对 (i, j) 中 0 <= i < nums1.length 且 0 <= j < nums2.length 。如果该下标对同时满足 i <= j 且 nums1[i] <= nums2[j] ，则称之为 有效 下标对，该下标对的 距离 为 j - i 。

返回所有 有效 下标对 (i, j) 中的 最大距离 。如果不存在有效下标对，返回 0 。

一个数组 arr ，如果每个 1 <= i < arr.length 均有 arr[i-1] >= arr[i] 成立，那么该数组是一个 非递增 数组。

示例 1：

输入：nums1 = [55,30,5,4,2], nums2 = [100,20,10,10,5] 输出：2 解释：有效下标对是 (0,0), (2,2), (2,3), (2,4), (3,3), (3,4) 和 (4,4) 。 最大距离是 2 ，对应下标对 (2,4) 。 示例 2：

输入：nums1 = [2,2,2], nums2 = [10,10,1] 输出：1 解释：有效下标对是 (0,0), (0,1) 和 (1,1) 。 最大距离是 1 ，对应下标对 (0,1) 。 示例 3：

输入：nums1 = [30,29,19,5], nums2 = [25,25,25,25,25] 输出：2 解释：有效下标对是 (2,2), (2,3), (2,4), (3,3) 和 (3,4) 。 最大距离是 2 ，对应下标对 (2,4) 。 示例 4：

输入：nums1 = [5,4], nums2 = [3,2] 输出：0 解释：不存在有效下标对，所以返回 0 。

提示：

1 <= nums1.length <= 10^5 1 <= nums2.length <= 10^5 1 <= nums1[i], nums2[j] <= 10^5 nums1 和 nums2 都是 非递增 数组

思路

二分查找。

代码

package JavaCode.contest.weekly.n201_300.n240;

public class N2 {
    public int maxDistance(int[] nums1, int[] nums2) {
        int res=0;
        for (int i=0;i<nums1.length;i++){
            if(i>=nums2.length)break;
            int j=find(nums2,i,nums1[i]);
            if(j!=-1){
                res=Math.max(j-i,res);
            }
        }
        return res;
    }

    private int find(int[] nums, int i, int tar) {
        if(nums[i]<tar)return -1;
        int l=i,r=nums.length-1;
        int res=i;
        while (l<=r){
            int mid=(l+r)/2;
            if(nums[mid]>=tar){
                res=Math.max(res,mid);
                l=mid+1;
            }
            else r=mid-1;
        }
        return res;
    }
}

题三 子数组最小乘积的最大值

描述

一个数组的 最小乘积 定义为这个数组中 最小值 乘以 数组的 和 。

比方说，数组 [3,2,5] （最小值是 2）的最小乘积为 2 * (3+2+5) = 2 * 10 = 20 。 给你一个正整数数组 nums ，请你返回 nums 任意 非空子数组 的最小乘积 的 最大值 。由于答案可能很大，请你返回答案对 109 + 7 取余 的结果。

请注意，最小乘积的最大值考虑的是取余操作 之前 的结果。题目保证最小乘积的最大值在 不取余 的情况下可以用 64 位有符号整数 保存。

子数组 定义为一个数组的 连续 部分。

示例 1：

输入：nums = [1,2,3,2] 输出：14 解释：最小乘积的最大值由子数组 [2,3,2] （最小值是 2）得到。 2 * (2+3+2) = 2 * 7 = 14 。 示例 2：

输入：nums = [2,3,3,1,2] 输出：18 解释：最小乘积的最大值由子数组 [3,3] （最小值是 3）得到。 3 * (3+3) = 3 * 6 = 18 。 示例 3：

输入：nums = [3,1,5,6,4,2] 输出：60 解释：最小乘积的最大值由子数组 [5,6,4] （最小值是 4）得到。 4 * (5+6+4) = 4 * 15 = 60 。

提示：

1 <= nums.length <= 10^5 1 <= nums[i] <= 10^7

思路

• 预处理sum。

• 依次遍历，假定当前值就是序列中的最小值，通过单调栈找到另一个边界计算即可。

代码

package JavaCode.contest.weekly.n201_300.n240;

import java.util.Stack;

public class N3 {
    public int maxSumMinProduct(int[] nums) {
        final int MOD= (int) (Math.pow(10,9)+7);
        long[] sum=new long[nums.length+1];
        for (int i=1;i<=nums.length;i++){
            sum[i]=sum[i-1]+nums[i-1];
        }
        long res=0;
        Stack<Integer> stack=new Stack<>();
        for (int i=0;i<nums.length;i++){
            while (!stack.isEmpty()&&nums[i]<=nums[stack.peek()]){
                int peek=stack.pop();
                int l=stack.isEmpty()?-1:stack.peek();
                res=Math.max(res, nums[peek] * (sum[i] - sum[l + 1]));
            }
            stack.push(i);
        }
        while (!stack.isEmpty()){
            int peek=stack.pop();
            int l=stack.isEmpty()?-1:stack.peek();
            res=Math.max(res, (sum[nums.length] - sum[l + 1]) *nums[peek]);
        }
        return (int) (res%MOD);
    }
}

题四 有向图中最大颜色值

描述

给你一个 有向图 ，它含有 n 个节点和 m 条边。节点编号从 0 到 n - 1 。

给你一个字符串 colors ，其中 colors[i] 是小写英文字母，表示图中第 i 个节点的 颜色 （下标从 0 开始）。同时给你一个二维数组 edges ，其中 edges[j] = [aj, bj] 表示从节点 aj 到节点 bj 有一条 有向边 。

图中一条有效 路径 是一个点序列 x1 -> x2 -> x3 -> ... -> xk ，对于所有 1 <= i < k ，从 xi 到 xi+1 在图中有一条有向边。路径的 颜色值 是路径中 出现次数最多 颜色的节点数目。

请你返回给定图中有效路径里面的 最大颜色值 。如果图中含有环，请返回 -1 。

示例 1：

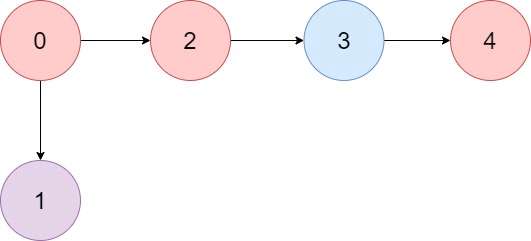
输入：colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]] 输出：3 解释：路径 0 -> 2 -> 3 -> 4 含有 3 个颜色为 "a" 的节点（上图中的红色节点）。 示例 2：

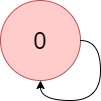
输入：colors = "a", edges = [[0,0]] 输出：-1 解释：从 0 到 0 有一个环。

提示：

n == colors.length m == edges.length 1 <= n <= 10^5 0 <= m <= 10^5 colors 只含有小写英文字母。 0 <= aj, bj < n

思路

拓扑排序加动态规划

• 如果存在环则不存在拓扑排序。

• 如果a->b，那么在拓扑排序中 b一定在a的后面，所以一条路径上点的顺序与拓扑排序的顺序是一致的。

• bash dp[next][color]=Math.mac(dp[next][color],dp[cur][color])

代码

import java.util.*;

public class N4 {
    public int largestPathValue(String colors, int[][] edges) {
        final int n=colors.length();
        final char[] c=colors.toCharArray();
        List<Integer>[] graph=new List[n];
        for (int i=0;i<n;i++)graph[i]=new ArrayList<>();

        int[] in=new int[n];
        for (int[] e:edges){
            in[e[1]]++;
            graph[e[0]].add(e[1]);
        }

        int found=0;
        Queue<Integer> queue=new ArrayDeque<>(n);
        for (int i=0;i<in.length;i++){
            if(in[i]==0)queue.add(i);
        }
        int[][] dp=new int[n][26];
        while (!queue.isEmpty()){
            int cur=queue.poll();
            found++;
            dp[cur][c[cur]-'a']++;
            for (int next:graph[cur]){
                in[next]--;
                if(in[next]==0)queue.add(next);
                for (int i=0;i<26;i++){
                    dp[next][i]=Math.max(dp[cur][i],dp[next][i]);
                }
            }
            if(found>n)return -1;
        }
        if(found!=n)return -1;
        int res=0;
        for (int[] d:dp){
            for (int i:d)res=Math.max(i,res);
        }

        return res;

    }


}