力扣第252场周赛

题一 三除数

描述

给你一个整数 n 。如果 n 恰好有三个正除数 ，返回 true ；否则，返回 false 。

如果存在整数 k ，满足 n = k * m ，那么整数 m 就是 n 的一个 除数 。

思路

直接遍历。。。

代码

public class N1 {
  public boolean isThree(int n) {
    int res = 0;
    for (int i=1;i<=n;i++){
      if(n%i==0)res++;
      if(res>3)return false;
    }
    return res==3;
  }
}

题二 你可以工作的最大周数

描述

给你 n 个项目，编号从 0 到 n - 1 。同时给你一个整数数组 milestones ，其中每个 milestones[i] 表示第 i 个项目中的阶段任务数量。

你可以按下面两个规则参与项目中的工作：

每周，你将会完成 某一个 项目中的 恰好一个 阶段任务。你每周都 必须 工作。 在 连续的 两周中，你 不能 参与并完成同一个项目中的两个阶段任务。 一旦所有项目中的全部阶段任务都完成，或者仅剩余一个阶段任务都会导致你违反上面的规则，那么你将 停止工作 。注意，由于这些条件的限制，你可能无法完成所有阶段任务。

返回在不违反上面规则的情况下你 最多 能工作多少周。

示例 1：

输入：milestones = [1,2,3] 输出：6 解释：一种可能的情形是： - 第 1 周，你参与并完成项目 0 中的一个阶段任务。

• 第 2 周，你参与并完成项目 2 中的一个阶段任务。

• 第 3 周，你参与并完成项目 1 中的一个阶段任务。

• 第 4 周，你参与并完成项目 2 中的一个阶段任务。

• 第 5 周，你参与并完成项目 1 中的一个阶段任务。

• 第 6 周，你参与并完成项目 2 中的一个阶段任务。 总周数是 6 。

示例 2:

输入：milestones = [5,2,1] 输出：7 解释：一种可能的情形是：

• 第 1 周，你参与并完成项目 0 中的一个阶段任务。
• 第 2 周，你参与并完成项目 1 中的一个阶段任务。
• 第 3 周，你参与并完成项目 0 中的一个阶段任务。
• 第 4 周，你参与并完成项目 1 中的一个阶段任务。
• 第 5 周，你参与并完成项目 0 中的一个阶段任务。
• 第 6 周，你参与并完成项目 2 中的一个阶段任务。
• 第 7 周，你参与并完成项目 0 中的一个阶段任务。 总周数是 7 。 注意，你不能在第 8 周参与完成项目 0 中的最后一个阶段任务，因为这会违反规则。 因此，项目 0 中会有一个阶段任务维持未完成状态。

思路

这题最初的想法也是贪心，不过贪的方向错了。

正确的思路：

如果阶段任务最多的项目可以完成，那么其他项目必定可以全部完成。

如果不可以完成，那么在剩余其它i个项目中可以填充i+1个位置给任务最多的项目,所以此时的周数为2*i+1。

直接计算两种情况，选小的那个就是真实情况。

代码

/**
 * @author mikusugar
 */
public class N2 {

  public long numberOfWeeks(int[] milestones) {
    long sum=0;
    long max=-1;
    for (int i:milestones){
      sum+=i;
      max=Math.max(i,max);
    }
    long i = sum-max;
    return Math.min(sum,i*2+1);
  }

}

题三 收集足够苹果的最小花园周长

描述

给你一个用无限二维网格表示的花园，每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。

你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ，且每条边都与两条坐标轴之一平行。

给你一个整数 neededApples ，请你返回土地的 最小周长 ，使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。

|x| 的值定义为：

如果 x >= 0 ，那么值为 x 如果 x < 0 ，那么值为 -x

示例 1：

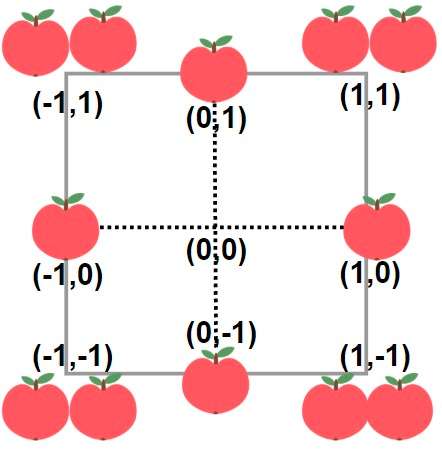
输入：neededApples = 1 输出：8 解释：边长长度为 1 的正方形不包含任何苹果。 但是边长为 2 的正方形包含 12 个苹果（如上图所示）。 周长为 2 * 4 = 8 。 示例 2：

输入：neededApples = 13 输出：16 示例 3：

输入：neededApples = 1000000000 输出：5040

思路

易得出最外一圈的计算公式，假设i为边离中心点的距离。

((i+2*i)*(i+1)-i)*4-(i*2)*4

代码

/**
 * @author mikusugar
 */
public class N3 {
  public long minimumPerimeter(long neededApples) {
    long sum=0;
    long res=0;
    while (sum<neededApples){
      res++;
      sum+=help(res);
    }
    return res*2*4;
  }

  private long help(long i) {
    return ((i+2*i)*(i+1)-i)*4-(i*2)*4;
  }
}

题四 统计特殊子序列的数目

描述

特殊序列 是由 正整数 个 0 ，紧接着 正整数 个 1 ，最后 正整数 个 2 组成的序列。

比方说，[0,1,2] 和 [0,0,1,1,1,2] 是特殊序列。 相反，[2,1,0] ，[1] 和 [0,1,2,0] 就不是特殊序列。 给你一个数组 nums （仅 包含整数 0，1 和 2），请你返回 不同特殊子序列的数目 。由于答案可能很大，请你将它对 109 + 7 取余 后返回。

一个数组的 子序列 是从原数组中删除零个或者若干个元素后，剩下元素不改变顺序得到的序列。如果两个子序列的 下标集合 不同，那么这两个子序列是 不同的 。

示例 1：

输入：nums = [0,1,2,2] 输出：3 解释：特殊子序列为 [0,1,2,2]，[0,1,2,2] 和 [0,1,2,2] 。 示例 2：

输入：nums = [2,2,0,0] 输出：0 解释：数组 [2,2,0,0] 中没有特殊子序列。 示例 3：

输入：nums = [0,1,2,0,1,2] 输出：7 解释：特殊子序列包括： - [0,1,2,0,1,2] - [0,1,2,0,1,2] - [0,1,2,0,1,2] - [0,1,2,0,1,2] - [0,1,2,0,1,2] - [0,1,2,0,1,2] - [0,1,2,0,1,2]

思路

最初错误的想法❌。

//最初的思路是DP，dp[3][nums.len],不过TimeOut了。
//超时的代码：
private final static int MOD = (int) (1e9+7);
  public int countSpecialSubsequences(int[] nums) {

    List<Integer>[] numslist = new List[3];
    for (int i=0;i<numslist.length;i++)numslist[i]=new ArrayList<>();

    for (int i=0;i<nums.length;i++){
      if(nums[i]==0)numslist[0].add(i);
      else if(nums[i]==1)numslist[1].add(i);
      else if(nums[i]==2)numslist[2].add(i);
    }


    long[][] dp = new long[3][nums.length];
    for (int i=0;i<3;i++) Arrays.fill(dp[i],-1);
    long res=0;
    for (int i=0;i< nums.length;i++){
      if(nums[i]==0){
        res+=slove(0,i, dp,numslist);
        res%=MOD;
      }
    }
    return (int) res;
  }

  private long slove(int num, int idx, long[][] dp, List<Integer>[] numslist) {
    if(dp[num][idx]!=-1)return dp[num][idx];
    long res=0;
    if(num==2)res++;
    for (int i=numslist[num].size()-1;i>=0&&numslist[num].get(i)>idx;i--){
      int next = numslist[num].get(i);
      res+=slove(num,next, dp,numslist);
    }
    if(num<2){
      for (int i=numslist[num+1].size()-1;i>=0&&numslist[num+1].get(i)>idx;i--){
        int next = numslist[num+1].get(i);
        res+=slove(num+1,next, dp,numslist);
      }
    }
    return dp[num][idx]=res;
  }

正确思路：

也是分为3种情况:

• 全是0的串 a
• 01组成的串 b
• 012组成的串 c

可以得到：

• 如果当前位是0,a+=a+1
• 如果当前位是1,b+=a+b
• 如果当前位是2,c+=b+c

代码

 private final static int MOD = (int) (1e9+7);
 public int countSpecialSubsequences(int[] nums) {
    int a=0,b=0,c=0;
    for (int i:nums){
      if(i==0){
        a+=a+1;
      }
      else if(i==1){
        b+=a+b;
      }
      else if(i==2){
        c+=b+c;
      }
    }
    return c;
 }

其它

太久没打了，虽然有两题解决的思路大体是一样的，但是想复杂了（就是菜。。。）