力扣第255场周赛
题一 找出数组的最大公约数
描述
给你一个整数数组 nums ,返回数组中最大数和最小数的 最大公约数 。
两个数的 最大公约数 是能够被两个数整除的最大正整数。
示例 1:
输入:nums = [2,5,6,9,10] 输出:2 解释: nums 中最小的数是 2 nums 中最大的数是 10 2 和 10 的最大公约数是 2 示例 2:
输入:nums = [7,5,6,8,3] 输出:1 解释: nums 中最小的数是 3 nums 中最大的数是 8 3 和 8 的最大公约数是 1 示例 3:
输入:nums = [3,3] 输出:3 解释: nums 中最小的数是 3 nums 中最大的数是 3 3 和 3 的最大公约数是 3
提示:
2 <= nums.length <= 1000 1 <= nums[i] <= 1000
思路
辗转相除法。
代码
/**
* @author mikusugar
*/
public class N1 {
public int findGCD(int[] nums) {
int min = Integer.MAX_VALUE;
int max = -1;
for (int i : nums) {
min = Math.min(min, i);
max = Math.max(max, i);
}
return gcd(min,max);
}
private int gcd(int n, int m) {
int t;
while (m > 0) {
t = n % m;
n = m;
m = t;
}
return n;
}
}
题二 找出不同的二进制字符串
描述
给你一个字符串数组 nums ,该数组由 n 个 互不相同 的二进制字符串组成,且每个字符串长度都是 n 。请你找出并返回一个长度为 n 且 没有出现 在 nums 中的二进制字符串。如果存在多种答案,只需返回 任意一个 即可。
示例 1:
输入:nums = ["01","10"] 输出:"11" 解释:"11" 没有出现在 nums 中。"00" 也是正确答案。 示例 2:
输入:nums = ["00","01"] 输出:"11" 解释:"11" 没有出现在 nums 中。"10" 也是正确答案。 示例 3:
输入:nums = ["111","011","001"] 输出:"101" 解释:"101" 没有出现在 nums 中。"000"、"010"、"100"、"110" 也是正确答案。
提示:
n == nums.length 1 <= n <= 16 nums[i].length == n nums[i] 为 '0' 或 '1'
思路
利用了字典树。
dfs暴力搜索到没有这样的前缀的时候给后续的位数添加0。
代码
/**
* @author mikusugar
*/
public class N2 {
public String findDifferentBinaryString(String[] nums) {
Node root = new Node();
for (String num : nums) {
buildTree(root, num.toCharArray());
}
final String ans = find(root, "", nums[0].length());
StringBuilder res = new StringBuilder(ans == null ? "" : ans);
for (int i = res.length(); i < nums[0].length(); i++) res.append('0');
return res.toString();
}
private String find(Node node, String s, final int n) {
if (node == null) {
if (s.length() <= n) return s;
return null;
}
final String res = find(node.one, s + '1', n);
if (res != null) return res;
return find(node.zero, s + '0', n);
}
private void buildTree(Node root, char[] strs) {
Node p = root;
for (char c : strs) {
if (c == '0') {
if (p.zero == null) p.zero = new Node();
p = p.zero;
} else {
if (p.one == null) p.one = new Node();
p = p.one;
}
}
}
static class Node {
Node zero;
Node one;
}
}
题三 最小化目标值与所选元素的差
描述
给你一个大小为 m x n 的整数矩阵 mat 和一个整数 target 。
从矩阵的 每一行 中选择一个整数,你的目标是 最小化 所有选中元素之 和 与目标值 target 的 绝对差 。
返回 最小的绝对差 。
a 和 b 两数字的 绝对差 是 a - b 的绝对值。
示例 1:
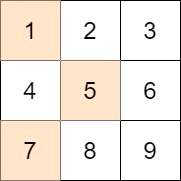
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13 输出:0 解释:一种可能的最优选择方案是: - 第一行选出 1
-
第二行选出 5
-
第三行选出 7 所选元素的和是 13 ,等于目标值,所以绝对差是 0 。
示例 2:

输入:mat = [[1],[2],[3]], target = 100 输出:94 解释:唯一一种选择方案是:
- 第一行选出 1
- 第二行选出 2
- 第三行选出 3 所选元素的和是 6 ,绝对差是 94 。
示例3:

输入:mat = [[1,2,9,8,7]], target = 6 输出:1 解释:最优的选择方案是选出第一行的 7 。 绝对差是 1 。
提示:
m == mat.length n == mat[i].length 1 <= m, n <= 70 1 <= mat[i][j] <= 70 1 <= target <= 800
思路
DFS 暴力剪枝优化。
代码
/**
* @author mikusugar
*/
public class N3 {
private int res;
public int minimizeTheDifference(int[][] mat, int target) {
Set<Integer>[] book = new Set[mat.length];
res = Integer.MAX_VALUE;
for (int i = 0; i < book.length; i++) book[i] = new HashSet<>();
dfs(0, 0, mat, book, target);
return res;
}
private void dfs(int sum, int level, int[][] mat, Set<Integer>[] book, int target) {
if (level == mat.length - 1) {
for (int i = 0; i < mat[level].length; i++) {
res = Math.min(res, Math.abs(target - sum - mat[level][i]));
}
return;
}
for (int i = 0; i < mat[level].length; i++) {
int s = sum + mat[level][i];
if (book[level].contains(s)) continue;
book[level].add(s);
dfs(s, level + 1, mat, book, target);
}
}
}
题四 从子集的和还原数组
描述
存在一个未知数组需要你进行还原,给你一个整数 n 表示该数组的长度。另给你一个数组 sums ,由未知数组中全部 2n 个 子集的和 组成(子集中的元素没有特定的顺序)。
返回一个长度为 n 的数组 ans 表示还原得到的未知数组。如果存在 多种 答案,只需返回其中 任意一个 。
如果可以由数组 arr 删除部分元素(也可能不删除或全删除)得到数组 sub ,那么数组 sub 就是数组 arr 的一个 子集 。sub 的元素之和就是 arr 的一个 子集的和 。一个空数组的元素之和为 0 。
注意:生成的测试用例将保证至少存在一个正确答案。
示例 1:
输入:n = 3, sums = [-3,-2,-1,0,0,1,2,3] 输出:[1,2,-3] 解释:[1,2,-3] 能够满足给出的子集的和: - []:和是 0 - [1]:和是 1 - [2]:和是 2 - [1,2]:和是 3 - [-3]:和是 -3 - [1,-3]:和是 -2 - [2,-3]:和是 -1 - [1,2,-3]:和是 0 注意,[1,2,-3] 的任何排列和 [-1,-2,3] 的任何排列都会被视作正确答案。 示例 2:
输入:n = 2, sums = [0,0,0,0] 输出:[0,0] 解释:唯一的正确答案是 [0,0] 。 示例 3:
输入:n = 4, sums = [0,0,5,5,4,-1,4,9,9,-1,4,3,4,8,3,8] 输出:[0,-1,4,5] 解释:[0,-1,4,5] 能够满足给出的子集的和。
提示:
1 <= n <= 15 sums.length == 2n -10^4 <= sums[i] <= 10^4
思路
没有。。。
代码
//TODO